Центр развития дополнительного образования имени Бернулли

Ликбез, глава 1. Подобные треугольники

Основные сведения

1.

Треугольник ABC подобен треугольнику A₁B₁C₁ (обозначение: DABC ~ DA₁B₁C₁) тогда и только тогда, когда выполнено одно из следующих эквивалентных условий:

а) AB : BC : CA = A₁B₁ : B₁C₁ : C₁A₁;

б) AB : BC = A₁B₁ : B₁C₁ и ÐABC = ÐA₁B₁C₁;

в) ÐABC = ÐA₁B₁C₁ и ÐBAC = ÐB₁A₁C₁.

2.

Если параллельные прямые отсекают от угла с вершиной A треугольники AB₁C₁ и AB₂C₂, то эти треугольники подобны и AB₁ : AB₂ = AC₁ : AC₂ (точки B₁ и B₂ лежат на одной стороне угла, C₁ и C₂ — на другой).

3.

Средней линией треугольника называют отрезок, соединяющий середины боковых сторон. Этот отрезок параллелен третьей стороне и равен половине ее длины.

Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции. Этот отрезок параллелен основаниям и равен полусумме их длин.

4.

Отношение площадей подобных треугольников равно квадрату коэффициента подобия, т. е. квадрату отношения длин соответствующих сторон. Это следует, например, из формулы

SABC =

1 2

AB · AC sin A

.

5.

Многоугольники A₁A₂… A_n и B₁B₂… B_n называют подобными , если A₁A₂ : A₂A₃ : …  : A_nA₁ = B₁B₂ : B₂B₃ : …  : B_nB₁ и углы при вершинах A₁,…, A_n равны соответственно углам при вершинах B₁, …, B_n.

Отношение соответственных диагоналей подобных многоугольников равно коэффициенту подобия; для описанных подобных многоугольников отношение радиусов вписанных окружностей также равно коэффициенту подобия.

Вводные задачи

1.

В остроугольном треугольнике ABC проведены высоты AA₁ и BB₁. Докажите, что A₁C · BC = B₁C · AC.

2.

В прямоугольном треугольнике ABC с прямым углом C проведена высота CH. Докажите, что AC² = AB · AH и CH² = AH · BH.

3.

Докажите, что медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2 : 1, считая от вершины.

4.

На стороне BC треугольника ABC взята точка A₁ так, что BA₁ : A₁C = 2 : 1. В каком отношении медиана CC₁ делит отрезок AA₁?

5.

В треугольник ABC вписан квадрат PQRS так, что вершины P и Q лежат на сторонах AB и AC, а вершины R и S — на стороне BC. Выразите длину стороны квадрата через a и h_a.

---

§ 1.  Отрезки, заключенные между параллельными прямыми

1.1.

Основания AD и BC трапеции ABCD равны a и b (a > b).

a) Найдите длину отрезка, высекаемого диагоналями на средней линии.

б) Найдите длину отрезка MN, концы которого делят стороны AB и CD в отношении AM : MB = DN : NC = p : q.

1.2.

Докажите, что середины сторон произвольного четырехугольника - вершины параллелограмма. Для каких четырехугольников этот параллелограмм является прямоугольником, для каких — ромбом, для каких — квадратом?

1.3.

а) Точки A₁ и B₁ делят стороны BC и AC треугольника ABC в отношениях BA₁ : A₁C = 1 : p и AB₁ : B₁C = 1 : q. В каком отношении отрезок AA₁ делится отрезком BB₁?

б) На сторонах BC и AC треугольника ABC взяты точки A₁ и B₁. Отрезки AA₁ и BB₁ пересекаются в точке D. Пусть a₁, b₁, c и d - расстояния от точек A₁, B₁, C и D до прямой AB. Докажите, что

1 a1

+

1 b1

=

1 c

+

1 d

.

1.4.

Через точку P медианы CC₁ треугольника ABC проведены прямые AA₁ и BB₁ (точки A₁ и B₁ лежат на сторонах BC и CA). Докажите, что A₁B₁||AB.

1.5.

Прямая, соединяющая точку P пересечения диагоналей четырехугольника ABCD с точкой Q пересечения прямых AB и CD, делит сторону AD пополам. Докажите, что она делит пополам и сторону BC.

1.6.

На стороне AD параллелограмма ABCD взята точка P так, что AP : AD = 1 : n; Q — точка пересечения прямых AC и BP. Докажите, что AQ : AC = 1 : (n + 1).

1.7.

Вершины параллелограмма A₁B₁C₁D₁ лежат на сторонах параллелограмма ABCD (точка A₁ лежит на стороне AB, точка B₁ - на стороне BC и т. д.). Докажите, что центры обоих параллелограммов совпадают.

1.8.

На диагонали BD параллелограмма ABCD взята точка K. Прямая AK пересекает прямые BC и CD в точках L и M. Докажите, что AK² = LK · KM.

1.9.

Одна из диагоналей вписанного в окружность четырехугольника является диаметром. Докажите, что проекции противоположных сторон на другую диагональ равны.

1.10.

На основании AD трапеции ABCD взята точка E так, что AE = BC. Отрезки CA и CE пересекают диагональ BD в точках O и P соответственно. Докажите, что если BO = PD, то AD² = BC²  +  AD · BC.

1.11.

Точки A и B высекают на окружности с центром O дугу величиной 60°. На этой дуге взята точка M. Докажите, что прямая, проходящая через середины отрезков MA и OB, перпендикулярна прямой, проходящей через середины отрезков MB и OA.

1.12.

а) Точки A, B и C лежат на одной прямой, а точки A₁, B₁, и C₁ — на другой. Докажите, что если AB₁||BA₁ и AC₁||CA₁, то BC₁||CB₁.

б) Точки A, B и C лежат на одной прямой, а точки A₁, B₁ и C₁ таковы, что AB₁||BA₁, AC₁||CA₁ и BC₁||CB₁. Докажите, что точки A₁, B₁ и C₁ лежат на одной прямой.

1.13.

В треугольнике ABC проведены биссектрисы AA₁ и BB₁. Докажите, что расстояние от любой точки M отрезка A₁B₁ до прямой AB равно сумме расстояний от M до прямых AC и BC.

1.14.

Пусть M и N — середины сторон AD и BC прямоугольника ABCD. На продолжении отрезка DC за точку D взята точка P; Q — точка пересечения прямых PM и AC. Докажите, что ÐQNM  =  ÐMNP.

1.15.

На продолжениях оснований AD и BC трапеции ABCD за точки A и C взяты точки K и L. Отрезок KL пересекает стороны AB и CD в точках M и N, а диагонали AC и BD в точках O и P. Докажите, что если KM = NL, то KO = PL.

1.16^*.

На сторонах AB, BC, CD и DA выпуклого четырехугольника ABCD взяты точки P, Q, R и S так, что BP : AB = CR : CD = a и AS : AD = BQ : BC = b. Докажите, что отрезки PR и QS делятся точкой их пересечения в отношениях b : (1 – b) и a : (1 – a).

---

§ 2.  Отношение сторон подобных треугольников

1.17.

а) В треугольнике ABC проведена биссектриса BD внутреннего или внешнего угла. Докажите, что AD : DC  =  AB : BC.

б) Докажите, что центр O вписанной окружности треугольника ABC делит биссектрису AA₁ в отношении AO : OA₁  =  (b + с) : a, где a, b, c — длины сторон треугольника.

1.18.

Длины двух сторон треугольника равны a, а длина третьей стороны равна b. Вычислите радиус его описанной окружности.

1.19.

Прямая, проходящая через вершину A квадрата ABCD, пересекает сторону CD в точке E и прямую BC в точке F. Докажите, что

1 AE^2

+

1 AF^2

=

1 AB^2

.

1.20.

На высотах BB₁ и CC₁ треугольника ABC взяты точки B₂ и C₂ так, что ÐAB₂C = ÐAC₂B = 90°. Докажите, что AB₂ = AC₂.

1.21.

В трапецию ABCD (BC||AD) вписана окружность, касающаяся боковых сторон AB и CD в точках K и L соответственно, а оснований AD и BC в точках M и N.

а) Пусть Q — точка пересечения отрезков BM и AN. Докажите, что KQ||AD.

б) Докажите, что AK · KB = CL · LD.

1.22.

На стороны BC и CD параллелограмма ABCD (или на их продолжение) опущены перпендикуляры AM и AN. Докажите, что DMAN ~ DABC.

1.23.

Прямая l пересекает стороны AB и AD параллелограмма ABCD в точках E и F соответственно. Пусть G — точка пересечения прямой l с диагональю AC. Докажите, что

AB AE

+

AD AF

=

AC AG

.

1.24.

Пусть AC — бóльшая из диагоналей параллелограмма ABCD. Из точки C на продолжения сторон AB и AD опущены перпендикуляры CE и CF соответственно. Докажите, что AB · AE + AD · AF = AC².

1.25.

Углы треугольника ABC связаны соотношением 3a +  2b  =  180°. Докажите, что a²  +  bc = c².

1.26.

Концы отрезков AB и CD перемещаются по сторонам данного угла, причем прямые AB и CD перемещаются параллельно; M — точка пересечения отрезков AB и CD. Докажите, что величина

AM · BM

---

CM · DM

остается постоянной.

1.27.

Через произвольною точку P стороны AC треугольника ABC параллельно его медианам AK и CL проведены прямые, пересекающие стороны BC и AB в точках E и F соответственно. Докажите, что медианы AK и CL делят отрезок EF на три равные части.

1.28.

На биссектрисе угла с вершиной C взята точка P. Прямая, проходящая через точку P, высекает на сторонах угла отрезки длиной a и b. Докажите, что величина

1 a

+

1 b

не зависит от выбора этой прямой.

1.29.

На стороне BC равностороннего треугольника ABC как на диаметре внешним образом построена полуокружность, на которой взяты точки K и L, делящие полуокружность на три равные дуги. Докажите, что прямые AK и AL делят отрезок BC на равные части.

Рис. 1.1

Рис. 1.2

1.30. Точка O — центр вписанной окружности треугольника ABC. На сторонах AC и BC выбраны точки M и K соответственно так, что BK · AB = BO² и AM · AB = AO². Докажите, что точки M, O и K лежат на одной прямой.

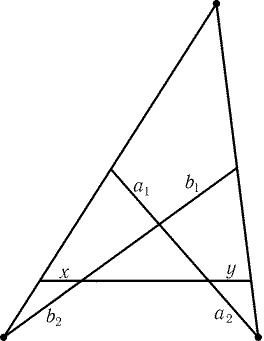
1.31^*. Докажите,  что  если  a₁ = a₂ и b₁ = b₂ (рис. 1.1), то x = y.

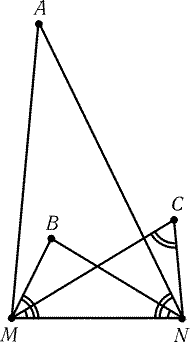
1.32^*. На отрезке MN построены подобные, одинаково ориентированные треугольники AMN, NBM и MNC (рис. 1.2). Докажите, что треугольник ABC подобен всем
этим треугольникам, а центр его описанной окружности равноудален от точек M и N.

1.33^*. Отрезок  BE  разбивает  треугольник ABC на два подобных треугольника, причем коэффициент подобия равен Ö3. Найдите углы треугольника ABC.

---

§ 3.  Отношение площадей подобных треугольников

1.34.

На стороне AC треугольника ABC взята точка E. Через точку E проведены прямая DE параллельно стороне BC и прямая EF параллельно стороне AB (D и E — точки соответственно на  этих сторонах). Докажите, что

SBDEF = 2

Ö

SADE · SEFC

.

1.35.

На боковых сторонах AB и CD трапеции ABCD взяты точки M и N так, что отрезок MN параллелен основаниям и делит площадь трапеции пополам. Найдите длину MN, если BC = a и AD = b.

1.36.

Через некоторую точку Q, взятую внутри треугольника ABC, проведены три прямые, параллельные его сторонам. Эти прямые разбивают треугольник на шесть частей, три из которых — треугольники с площадями S₁, S₂ и S₃. Докажите, что площадь треугольника ABC равна

(

Ö

S1

+

Ö

S2

+

Ö

S3

)^2.

1.37.

Докажите, что площадь треугольника, стороны которого равны медианам треугольника площади S, равна 3S / 4.

1.38.

а) Докажите, что площадь четырехугольника, образованного серединами сторон выпуклого четырехугольника ABCD, равна половине площади ABCD.

б) Докажите, что если диагонали выпуклого четырехугольника равны, то его площадь равна произведению длин отрезков, соединяющих середины противоположных сторон.

1.39.

Точка O, лежащая внутри выпуклого четырехугольника площади S, отражается симметрично относительно середин его сторон. Найдите площадь четырехугольника с вершинами в полученных точках.

---

§ 4.  Вспомогательные равные треугольники

1.40.

Катет BC прямоугольного треугольника ABC с прямым углом C разделен точками D и E на три равные части. Докажите, что если BC = 3AC, то сумма углов AEC, ADC и ABC равна 90°.

1.41.

Точка K — середина стороны AB квадрата ABCD, а точка L делит диагональ AC в отношении AL : LC = 3 : 1. Докажите, что угол KLD прямой.

1.42.

Через вершину A квадрата ABCD проведены прямые l₁ и l₂, пересекающие его стороны. Из точек B и D опущены перпендикуляры BB₁, BB₂, DD₁ и DD₂ на эти прямые. Докажите, что отрезки B₁B₂ и D₁D₂ равны и перпендикулярны.

1.43.

На катетах CA и CB равнобедренного прямоугольного треугольника ABC выбраны точки D и E так, что CD = CE. Продолжения перпендикуляров, опущенных из точек D и C на прямую AE, пересекают гипотенузу AB в точках K и L. Докажите, что KL = LB.

1.44^*.

На сторонах AB, BC, CD и DA вписанного четырехугольника ABCD, длины которых равны a, b, c и d, внешним образом построены прямоугольники размером a×с, b×d, с×а и d×b. Докажите, что их центры являются вершинами прямоугольника.

1.45^*.

Шестиугольник ABCDEF вписан в окружность радиуса R с центром O, причем AB = CD = EF = R. Докажите, что точки попарного пересечения описанных окружностей треугольников BOC, DOE и FOA, отличные от точки O, являются вершинами правильного треугольника со стороной R.

*       *      *

1.46.

На сторонах BC и CD параллелограмма ABCD построены внешним образом правильные треугольники BCK и DCL. Докажите, что треугольник AKL правильный.

1.47.

На сторонах параллелограмма внешним образом построены квадраты. Докажите, что их центры образуют квадрат.

1.48^*.

На сторонах произвольного треугольника ABC внешним образом построены равнобедренные треугольники с углами 2a, 2b и 2g при вершинах A¢, B¢ и C¢, причем a + b + g  =  180°. Докажите, что углы треугольника A¢B¢C¢ равны a, b и g.

1.49^*.

На сторонах треугольника ABC как на основаниях построены подобные равнобедренные треугольники AB₁С и AC₁B внешним образом и BA₁C внутренним образом. Докажите, что AB₁A₁C₁ — параллелограмм.

1.50^*.

а) На сторонах AB и AC треугольника ABC внешним образом построены прямоугольные треугольники ABC₁ и AB₁C, причем ÐC₁ = ÐB₁ = 90°, ÐABC₁  =  ÐACB₁ = j; M — середина BC. Докажите, что MB₁ = MC₁ и ÐB₁ M C₁ = 2j.

б) На сторонах треугольника ABC внешним образом построены правильные треугольники. Докажите, что их центры образуют правильный треугольник, причем его центр совпадает с точкой пересечения медиан треугольника ABC.

1.51^*.

На неравных сторонах AB и AC треугольника ABC внешним образом построены равнобедренные треугольники AC₁B и AB₁C с углом j при вершине.

а) M — точка медианы AA₁, (или ее продолжения), равноудаленная от точек B₁ и C₁. Докажите, что ÐB₁MC₁ = j.

б) O — точка серединного перпендикуляра к отрезку BC, равноудаленная от точек B₁ и C₁. Докажите, что ÐB₁OC₁  =  180°  – j.

1.52^*.

На сторонах выпуклого четырехугольника ABCD внешним образом построены подобные ромбы, причем их острые углы a прилегают к вершинам A и C. Докажите, что отрезки, соединяющие центры противоположных ромбов, равны, а угол между ними равен a.

---

§ 5.  Треугольник, образованный основаниями высот

1.53.

Пусть AA₁ и BB₁ — высоты треугольника ABC. Докажите, что DA₁B₁C ~ DABC. Чему равен коэффициент подобия?

1.54.

Из вершины C остроугольного треугольника ABC опущена высота CH, а из точки H опущены перпендикуляры HM и HN на стороны BC и AC соответственно. Докажите, что D MNC ~ DABC.

1.55.

В треугольнике ABC проведены высоты BB₁ и CC₁.

а) Докажите, что касательная в точке A к описанной окружности параллельна прямой B₁C₁.

б) Докажите, что B₁C₁^OA, где O — центр описанной окружности.

1.56.

На сторонах остроугольного треугольника ABC взяты точки A₁, B₁ и C₁ так, что отрезки AA₁, BB₁ и CC₁ пересекаются в точке H. Докажите, что AH · A₁H = BH · B₁H = CH · C₁H тогда и только тогда, когда H — точка пересечения высот треугольника ABC.

1.57.

а) Докажите, что высоты AA₁, BB₁ и CC₁ остроугольного треугольника ABC делят углы треугольника A₁B₁C₁ пополам.

б) На сторонах AB, BC и CA остроугольного треугольника ABC взяты точки C₁, A₁ и B₁ соответственно. Докажите, что если ÐB₁A₁C = ÐBA₁C₁, ÐA₁B₁C = ÐAB₁C₁ и ÐA₁C₁B = ÐAC₁B₁, то точки A₁, B₁ и C₁ являются основаниями высот треугольника ABC.

1.58.

В остроугольном треугольнике ABC проведены высоты AA₁, BB₁ и CC₁. Докажите, что точка, симметричная A₁ относительно прямой AC, лежит на прямой B₁C₁.

1.59.

В остроугольном треугольнике ABC проведены высоты AA₁, BB₁ и CC₁. Докажите, что если A₁B₁||AB и B₁C₁||BC, то A₁C₁||AC.

1.60^*.

Пусть p — полупериметр остроугольного треугольника ABC, q — полупериметр треугольника, образованного основаниями его высот. Докажите, что p : q = R : r, где R и r — радиусы описанной и вписанной окружностей треугольника ABC.

---

§ 6.  Подобные фигуры

1.61.

В треугольник вписана окружность радиуса r. Касательные к этой окружности, параллельные сторонам треугольника, отсекают от него три маленьких треугольника. Пусть r₁, r₂, r₃ — радиусы вписанных в эти треугольники окружностей. Докажите, что r₁ + r₂ + r₃ = r.

1.62.

Дан треугольник ABC. Постройте две прямые x и y так, чтобы для любой точки M на стороне AC сумма длин отрезков MX_M и MY_M, проведенных из точки M параллельно прямым x и y до пересечения со сторонами AB и BC треугольника, равнялась 1.

1.63.

В равнобедренном треугольнике ABC из середины H основания BC опущен перпендикуляр HE на боковую сторону AC; O — середина отрезка HE. Докажите, что прямые AO и BE перпендикулярны.

1.64.

Докажите, что проекции основания высоты треугольника на стороны, ее заключающие, и на две другие высоты лежат на одной прямой.

1.65.

На отрезке AC взята точка B и на отрезках AB, BC, CA построены полуокружности S₁, S₂, S₃ по одну сторону от AC. D — такая точка на S₃, что BD^AC. Общая касательная к S₁ и S₂, касается этих полуокружностей в точках F и E соответственно.

а) Докажите, что прямая EF параллельна касательной к S₃, проведенной через точку D.

б) Докажите, что BFDE — прямоугольник.

1.66^*.

Из произвольной точки M окружности, описанной около прямоугольника ABCD, опустили перпендикуляры MQ и MP на его две противоположные стороны и перпендикуляры MR и MT на продолжения двух других сторон. Докажите, что прямые PR и QT перпендикулярны, а точка их пересечения принадлежит диагонали прямоугольника ABCD.

1.67^*.

К двум окружностям, расположенным одна вне другой, проведены одна внешняя и одна внутренняя касательные. Рассмотрим две прямые, каждая из которых проходит через точки касания, принадлежащие одной из окружностей. Докажите, что точка пересечения этих прямых расположена на прямой, соединяющей центры окружностей.

---

Задачи для самостоятельного решения

1.68.

Основание равнобедренного треугольника составляет четверть его периметра. Из произвольной точки основания проведены прямые, параллельные боковым сторонам. Во сколько раз периметр треугольника больше периметра отсеченного параллелограмма?

1.69.

Диагонали трапеции взаимно перпендикулярны. Докажите, что произведение длин оснований трапеции равно сумме произведений длин отрезков одной диагонали и длин отрезков другой диагонали, на которые они делятся точкой пересечения.

1.70.

Сторона квадрата равна 1. Через его центр проведена прямая. Вычислите сумму квадратов расстояний от четырех вершин квадрата до этой прямой.

1.71.

Точки A₁, B₁ и C₁ симметричны центру описанной окружности треугольника ABC относительно его сторон. Докажите, что DABC = DA₁B₁C₁.

1.72.

Докажите, что если ÐBAC = 2ÐABC, то BC² = (AC + AB) · AC.

1.73.

На прямой l даны точки A, B, C и D. Через точки A и B, а также через точки C и D проводятся параллельныe прямые. Докажите, что диагонали полученных таким образом параллелограммов (или их продолжения) пересекают прямую l в двух фиксированных точках.

1.74.

В треугольнике ABC проведены биссектриса AD и средняя линия A₁C₁. Прямые AD и A₁C₁ пересекаются в точке K. Докажите, что 2A₁K = |b – c|.

1.75.

На сторонах AD и CD параллелограмма ABCD взяты точки M и N так, что MN||AC. Докажите, что S_ABM = S_CBN.

1.76.

На диагонали AC параллелограмма ABCD взяты точки P и Q так, что AP = CQ. Точка М такова, что PM||AD и QM||AB. Докажите, что точка M лежит на диагонали BD.

1.77.

Продолжения боковых сторон трапеции с основаниями AD и BC пересекаются в точке O. Концы отрезка EF, параллельного основаниям и проходящего через точку пересечения диагоналей, лежат соответственно на сторонах AB и CD. Докажите, что AE : CF = AO : CO.

1.78.

Три прямые, параллельные сторонам данного треугольника, отсекают от него три треугольника, причем остается равносторонний шестиугольник. Найдите длину стороны шестиугольника, если длины сторон треугольника равны a, b и c.

1.79.

Три прямые, параллельные сторонам треугольника, пересекаются в одной точке, причем стороны треугольника высекают на этих прямых отрезки длиной x. Найдите x, если длины сторон треугольника равны a, b и c.

1.80.

Точка P лежит внутри треугольника ABC, причем ÐABP = ÐACP. На прямых AB и AC взяты такие точки C₁, и B₁, что BC₁ : CB₁ = CP : BP. Докажите, что одна из диагоналей параллелограмма, две стороны которого лежат на прямых BP и CP, а две другие стороны (или их продолжение) проходят через B₁ и C₁, параллельна BC.

---